Formalizing the modeling language – Introduction

To be able to reason about your models through the back-end, it is necessary to have a definition of their semantics. Concretely, the semantics specifies the logical “meaning” of your model, and, in particular, what interests us for this application is that this meaning be executable so that we can run queries w.r.t. the semantics. The back-end utilizes several finite-domain constraint solvers to analyze the models and extract information. The exact mechanism for querying your model will be detailed in the Writing Queries section of this wiki.

To begin, it is necessary to determine what the logical semantics of your model are, either by looking for proposals in the literature or by otherwise defining them yourself if you are working with a new/unique/extended language. In particular, these semantics must be expressible in such a way that the logical theory they produce constitutes a constraint satisfaction problem over the finite domain of integers/booleans. Your semantics must therefore be based on the abstract syntax of your language, in such a way that your models can then be translated into a logical theory, whose “models” (in the model-theoretic sense) will correspond to satisfying assignments of the variables associated to the abstract syntactic elements of your model.

Once such a formalization of the language has been constructed, it is possible to begin defining the semantics of the language for use by the semantic translator. To do this, your language must first have a complete definition of its abstract syntax within VariaMos. Once this has been done, we can begin associating the semantics to the models.

A first example – Feature Models

Feature models have well defined semantics that have been presented in many occasions in the literature. For now, we will not delve into the attributes extension to these models, nor into the semantics of individual cardinalities for features, though both can be expressed (the reason for this omission is that not only does this bring added complexity but it also has implications for solver behavior when enumerating solutions).

The figure above presents a feature model with an intentional defects (it is in fact void). To able to detect these defects through automated analysis we must be able to express the semantics of the different types of constructions that exist within feature models. Let us then first consider the abstract syntax of the language so that we can have a clearer picture of the constituent components of Feature Models.

{
    "elements": {
      "Bundle": {"properties": [...,{"name": "Type","possibleValues": "And,Or,Xor,Range",...},...]},
      "RootFeature": {"properties": [...,{"name": "Selected",...}]},
      "AbstractFeature": {"properties": [...,{"name": "Selected",...}]},
      "ConcreteFeature": {
        "properties": [...,{"name": "Selected",...}]}
    },
    "relationships": {
      "Bundle_Feature": {"source": "Bundle","target": ["AbstractFeature","ConcreteFeature"],...},
      "RootFeature_Bundle": {"source": "RootFeature","target": ["Bundle"],...},
      "RootFeature_Feature": {
        "source": "RootFeature", "target": ["AbstractFeature","ConcreteFeature"],
        "properties": [
          {
            "name": "Type",
            "possibleValues": "Mandatory,Optional,Includes,Excludes,..."
          },...
        ]
      },
      "AbstractFeature_Bundle": {"source": "AbstractFeature","target": ["Bundle"],...},
      "ConcreteFeature_Bundle": {"source": "ConcreteFeature","target": ["Bundle"],...},
      "AbstractFeature_Feature": {
        "source": "AbstractFeature", "target": ["AbstractFeature","ConcreteFeature"],
        "properties": [
          {
            "name": "Type",
            "possibleValues": "Mandatory,Optional,Includes,Excludes,..."
          },...
        ]
      },
      "ConcreteFeature_Feature": {
        "source": "ConcreteFeature", "target": ["ConcreteFeature","AbstractFeature"],
        "properties": [
          {
            "name": "Type",
            "possibleValues": "Mandatory,Optional,Includes,Excludes,..."
          },...
        ]
      }
    }
  }

On the basis of this abstract syntax we can begin to construct the representation of our model in CLIF. Our goal is to provide a representation in logic for each semantically significant element of the model.

Defining the translation for elements

“elementTypes” and “elementTranslationRules”

The simplest translation that can be done is to directly represent a model element as a formula. This formula can only draw upon the information of the element, though it can also make use of the properties to, e.g., generate the symbols for an enumeration, in which case we can specify this as well. Simply put, all we’re doing is defining which element types (i.e. the types declared in the abstract syntax) are going to be translated only on their own basis. We define these types in the “element_types” attribute which is a list of these types.

For each of the types in that list, we define a set of (object) attributes that specify how to construct the CLIF formulas from the information in the model. We have one attribute named param that defines the placeholder for the element’s ID in the actual formula.
With this placeholder, we can then write the constraint attribute, which specifies the actual CLIF formula providing the semantics.
In general, when it comes to the elements themselves, we use their translation as a way to use their IDs as finite domain variables for the solver (since this is what interests us after all). We therefore translate them as unary predicates that serve as type constraints on these variables. In the specific case of enumerations, the type constraint predicate is actually binary, since we need to define the allowed symbols for the enumeration. With this in mind, we can take these values from one of the properties defined on the element. In this case, there is an attribute named enumMapping that takes its values from the PossibleValues property (searched by name, so make sure your properties have unique names for a given element type), and then provide a placeholder which will be used in the constraint to define the list of symbols in the enumeration. We do expect the property to be declared (FOR NOW) as having a String type and having a set of values in a single string connected by commas with no spaces. For now the predicates we can handle for the types are:

• (bool <someID>) Boolean variable.
• `(enum () ) Enumeration Variable.
• (int <someID>) Integer Variable.

Let’s now examine how we translate the three types of features available in our Feature Model:

"elementTypes": [
  "ConcreteFeature",
  "RootFeature",
  "AbstractFeature"
],
"elementTranslationRules": {
  "RootFeature": {
    "param": "F",
    "constraint": "(and (bool UUID_F) (= UUID_F 1))",
    "selectedConstraint": "(and (bool UUID_F) (= UUID_F 1))",
    "deselectedConstraint": "(= 0 1)"
  },
  "AbstractFeature": {
    "param": "F",
    "constraint": "(bool UUID_F)",
    "selectedConstraint": "(and (bool UUID_F) (= UUID_F 1))",
    "deselectedConstraint": "(and (bool UUID_F) (= UUID_F 0))"
  },
  "ConcreteFeature": {
    "param": "F",
    "constraint": "(bool UUID_F)",
    "selectedConstraint": "(and (bool UUID_F) (= UUID_F 1))",
    "deselectedConstraint": "(and (bool UUID_F) (= UUID_F 0))"
  }
},

Here we first define an attribute elementTypes that contains a list of all the element types that are to be translated. Note that we have not yet talked about the bundles, since they are translated in a different manner. So, for now, we focus primarily only on the features.
With this done, we define the elementTranslationRules, an object whose attributes define how each of the element types define before in the elementTypes list is translated into a CLIF sentence. Considering what was mentioned before, it should be clear that each feature type has its own equation template. In this case we prepend UUID_ to the template since translations into the solvers require that we guarantee that a letter is the first character of a variable, moreover, for SWI-Prolog in particular, it must be a capital letter, hence we simply add this prefix to ensure that everything is represented correctly for the solvers. NOTE: This is a temporary restriction and will be fixed in a future release.

In the case of feature models, since selection status is a special property that is highly important, we also provide two additional attributes that can be set: selectedConstraint and deselectedConstraint which are alternative constraints that are used in place of the default constraint in case a feature has been selected or deselected respectively.

Attributes, Individual Cardinalities, and hierarchyTypes and hierarchyTranslationRules

NOTE: These will be presented in the second example case. For various reasons, the behavior of the solvers when attributes are present on feature models is less than ideal, in particular, they will simply cycle through all the possible values of the attributes as distinct solutions instead of enumerating different feature combinations as a priority. It is for this reason that while available, it is not yet desirable to use the features attribute’s for analysis

NOTE 2: Individual cardinalities pose similar problems as before. These are available in the semantics but they involve some more complex manipulations that are unnecessary for a basic understanding of the system, they are therefore ignored for now

NOTE 3: There exist translation rules for elements whose translation is sensitive to their position in a tree-like hierarchy, like the root features, but that require information about their parents/descendants. Therefore, for now, these are not used for feature models but are a required parameter for the semantics specification, they are therefore just listed as empty.

"hierarchyTypes":[],
"hierarchyTranslationRules":{},

“relationTypes”, “relationTranslationRules” and “relationPropertySchema”

These rules are designed specifically to provide translations for edges between nodes in the model. We suppose the edges themselves have no variable associated to them and instead, we obtain two bindings. The first is that of the source of the edge and the second is always bound to the target of the edge. We can then use these nodes’ IDs in the constraint.

"relationTypes": [
  "Mandatory",
  "Optional",
  "Includes",
  "Excludes"
  "Range",
  "Xor",
  "And",
  "Or"
],
"relationPropertySchema": {
  "type": {
    "index": 0,
    "key": "value"
  }
},
"relationTranslationRules": {
  "Excludes": {
    "params": [
      "F1",
      "F2"
    ],
    "constraint": "(=< (UUID_F1 + UUID_F2) 1)"
  },
  "Includes": {
    "params": [
      "F1",
      "F2"
    ],
    "constraint": "(>= UUID_F2 UUID_F1)"
  },
  "Optional": {
    "params": [
      "F1",
      "F2"
    ],
    "constraint": "(>= UUID_F1 UUID_F2)"
  },
  "Mandatory": {
    "params": [
      "F1",
      "F2"
    ],
    "constraint": "(= UUID_F1 UUID_F2)"
  }
}

It’s important to recognize that feature models type the relations through an attribute of the relation. For this reason, we provide a special attribute in the semantic definition relationPropertySchema whose attribute type tells the system that instead of using the default relation type to determine the type of the relation, it must perform a lookup on the properties of the relation to determine its type. These allowed types are then listed in the list relationTypes. Concretely, this definition defines that it must look in the properties list of the relation and check the 1st (0 in programming order) element, and lookup the attribute whose key is value. NOTE: This is unfortunately tied to limitations of the mxgraph system, and will hopefully be improved in a future release.

“relationReificationTypes”, “relationReificationTranslationRules”, “relationReificationTypeDependentExpansions”, “relationReificationPropertySchema”, and “relationReificationExpansions”

Here we come to the more complex translations, specifically those that have represent reified relations. This has several meanings, and has been designed so that we can accomodate both of the potential cases. Concretely, by reified relation we mean elements that represent a many-to-many, many-to-one or one-to-many relationship between other elements. The two possible cases are whether the relationship itself has a value and corresponding variable or not. This is not the case for bundles in Feature Models that merely represent one to many relationships.

First, relationReificationTypes is, as before, a list representing the types that will be treated in this manner. Next, we come to the relationReificationTranslationRules, where we continue with the earlier pattern, and associate an object to each type we declared before. Here we have a parameter list (param) and a mapping for these parameters (paramMapping) that behave in such a manner that we make one mapping for incoming edges and one for outgoing. Either of these can be a single edge, where we’d mark the mapping with "unique": true. Finally, another special characteristic of the constraints we can employ here, is the fact that we can have additional parameters that benefit from a lookup within the element’s attributes, as is the case of the Bundle elements in Feature Models. When we mark a variable as not being unique, it is to be understood as a list.

To obtain, for example, the min value for the Cardinality elements, we define first in "relationReificationTypeDependentExpansions" the types that will have these additional expansions and then we provide a lookup schema in "relationReificationPropertySchema", which basically explains where to look in the element’s properties for the value to replace the placeholder with as was explained in an earlier section. This unfortunately means, that for now, at least, a minimal understanding of how the properties will be indexed by VariaMos is necessary. In addition, we define the more general expansions related to the nodes our element is connected with. In this case we declare that we will have the len and sum expansions, which are those that have been defined so far:

• sum(<Var>) will transform the list that corresponds to Var into an actual sum, and thus this will create a sum constraint over the IDs contained in the list, i.e. UUID_F1 + UUID_F2 and so on.
• len(<Var>) will replace itself with the number of elements in the list.

Finally, it is worth noting that since the bundle can have multiple types, it has been defined that the constraint can be an object and not just a string. Therefore, the relationReificationPropertySchema‘s definition of ‘type’ will be used to determine the correct constraint to apply given the type defined in the attibute. NOTE: This behavior is therefore different from that used for determining the types of the other relations and unfortunately is again tied to limitations of how VariaMos Types elements.

"relationReificationTypes": [
  "Bundle"
],
"relationReificationTranslationRules":{
  "Bundle": {
    "param": [
      "F",
      "Xs",
      "min",
      "max"
    ],
    "paramMapping": {
      "inboundEdges": {
        "unique": true,
        "var": "F"
      },
      "outboundEdges": {
        "unique": false,
        "var": "Xs"
      }
    },
    "constraint": {
      "Or": "(and (=< F (sum(Xs))) (=< (sum(Xs)) (F * len(Xs))) )",
      "And": "(= (sum(Xs)) (F * len(Xs)))",
      "Xor": "(= (sum(Xs)) F )",
      "Range": "(and (=< (F * min) (sum(Xs))) (=< (sum(Xs)) (F * max)) )"
    }
  }
},
"relationReificationTypeDependentExpansions": {
  "Bundle": {
    "Range": [
      "max",
      "min"
    ]
  }
},
"relationReificationPropertySchema": {
  "type": {
    "index": 0,
    "key": "value"
  },
  "min": {
    "index": 1,
    "key": "value"
  },
  "max": {
    "index": 2,
    "key": "value"
  }
},
"relationReificationExpansions": {
  "params": [
    "Xs"
  ],
  "functions": [
    "sum",
    "len"
  ]
},

A second example case – RECOCOS

We will examine the construction of the logical semantics of a complex language, namely the RECOCOS language that is an evolution of the KAOS variant presented in “Using constraint programming to manage configurations in self-adaptive systems” by Sawyer et al.

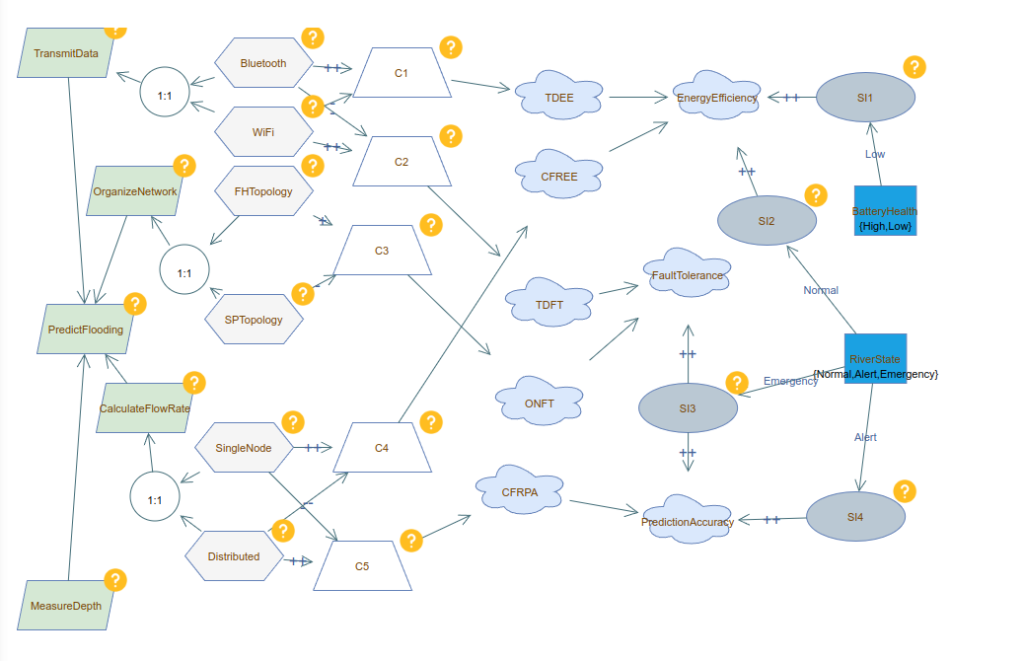
Here is the model reconstructed in VariaMos:

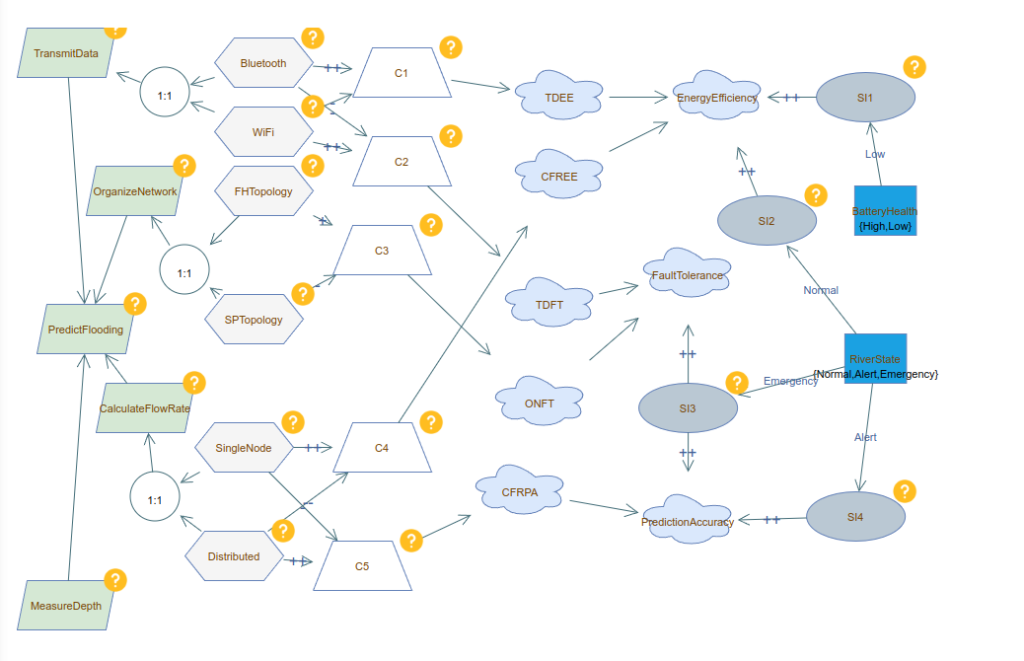
Here is an abbreviated version of the abstract syntax including the primary elements that interest us:

{
  "elements": {
    "Goal": { "properties": [...,{ "name": "Selected", ... }] },
    "Claim": { "properties": [...,{ "name": "Selected", ... }] },
    "SoftGoal": {...},
    "Cardinality": {"properties": [{"name": "From",...},{"name": "To",...}]},
    "SoftInfluence": { "properties": [...,{ "name": "Selected", ... }] },
    "ContextVariable": {"properties": [{"name": "SetValue",...},{"name": "PossibleValues",...}]},
    "Operationalization": { "properties": [...,{ "name": "Selected", ... }] },
  },
  "restrictions": {},
  "relationships": {
    "SubGoal": {..., "source": "Goal", "target": ["Goal"],},
    "SoftGoal_SoftGoal": {...},
    "Claim_SoftGoal": {...},
    "Cardinality_Goal": {...},
    "SoftInfluence_SoftGoal": {...,
      "properties": [{..., "name": "SatisfactionLevel","possibleValues": "--,-,=,+,++"}]},
    "ContextVariable_SoftInfluence": { ..., "properties": [{"name": "Value",...}] },
    "Operationalization_Claim_Goal": {..., "properties": [{"name": "Value", "possibleValues": " ,--,-,=,+,++" }]}
  }
}

Once again, on the basis of this abstract syntax we can begin to construct the representation of our model in CLIF.

Building the RECOCOS semantics specification JSON

The JSON we must construct is composed of a series of attributes that define how the translations are to be carried out. We will analyze step by step how to write the translation rules for this language by going over the complete example of the RECOCOS language.

Keep in mind that every attribute we’ll examine will be part of a larger object which forms the complete semantics specification. So to use the example provided below, you would need to combine all of these subsections.

“elementTypes” and “elementTranslationRules”

As explained before for feature models, we provide the translation of the elements that depend only on themselves and their attributes.

Here then, we present the translations of three element types, Goals (Green parallelograms on the left) and Operationalizations (hexagons), which correspond to boolean variables in the semantics, and Context Variables (blue squares) which correspond to enumerations.

"elementTypes": [
  "ContextVariable",
  "Goal",
  "Operationalization"
],
"elementTranslationRules": {
  "ContextVariable": {
    "param": "C",
    "constraint": "(enum (Xs) UUID_C)",
    "enumMapping": {
      "var": "Xs",
      "attribute":"PossibleValues"
    }
  },
  "Goal": {
    "param": "F",
    "constraint": "(bool UUID_F)"
  },
  "Operationalization": {
    "param": "F",
    "constraint": "(bool UUID_F)"
  }
},

“attributeTypes” and “attributeTranslationRules”

These two attributes work in a very similar way as the two above for the elements themselves. However, they are designed to provide translations for the properties associated to elements. They exist as a separate translation rule-set since not every language will necessarily need to use the properties for translation. The attributeTypes attribute defines the element types (i.e., as before, the types declared in the abstract syntax) for which the properties should be translated. For now we assume a homogeneous treatment of all the attributes with the same name, if they were to occur in multiple elements of different types (though this might change to better reflect other types of models).

The attributeTranslationRules attribute defines, just like the elementTranslationRules attribute above, how to transform a given attribute into a CLIF formula. In this case, since RECOCOS needs some specific values for the context for it to be able to search for an optimal configuration, we have a property that defines the current value of the context variable (whose possible values come from the enumeration that is translated in the subsection above) named SetValue. It acts just like the constraint defined above, with the sole difference of being able to refer to the element’s id through the parent attribute that provides a placeholder name for it. The param attribute defines which field in the property will provide the concrete value that the template placeholder will replace.

"attributeTypes": ["ContextVariable"],
"attributeTranslationRules": {
  "SetValue": {
    "parent": "C",
    "param": "value",
    "template": "V",
    "constraint": "(= UUID_C V)"
  }
},

“hierarchyTypes” and “hierarchyTranslationRules”

Next we have another type of translation that we may need to construct for certain languages, which is, in particular, necessary for our case: hierarchies. In this case, we envisage elements whose translation may vary depending on whether or not they are at the root or at the leaves of a hierarchical (tree-like) structure. For the RECOCOS model this is the case for the SoftGoals. We have a type definition as before through the hierarchyTypes attribute.

Once we’ve defined these types, we define the translation rules depending on whether or not an element is a leaf in the hierarchy (Note that there may be several of these hierarchies). Simply put, the leafRule attribute contains a definitions that works exactly the same as it does in the elementTranslationRules. For the nodeRule attribute, however, we must have an object that defines two parameters (placeholders for the constraint): the first, corresponding to the node’s ID, and, another, that will use information from the nodes one level down (or up, depending on how the hierarchy is constructed). An additional attribute named paramMapping defines how the information for both the node’s ID and those of the other nodes in the hierarchy are related to the placeholders. Inside this paramMapping attribute, node corresponds to the placeholder for the node’s own ID and var is for the list of the other nodes, with incoming determining whether the hierarchy is looked for in the incoming or outgoing edges (since the node can also connect with other nodes of different types).

Finally, with these mappings, a constraint can be written. This constraint can also use a series of expansions that have been defined and that operate on the lists of other nodes. For now we have defined:

• sum(<Var>) will transform the list that corresponds to Var into an actual sum, and thus this will create a sum constraint over the IDs contained in the list.
• len(<Var>) will replace itself with the number of elements in the list.

These expansions are treated in a bit more detail in the following subsection. Here we create a constraint that says as you go up the hierarchy, a nodes value is the average of those underneath, or its own value if it’s a leaf in the hierarchy.

"hierarchyTypes": [
  "SoftGoal"
],
"hierarchyTranslationRules": {
  "SoftGoal": {
    "nodeRule": {
      "param": [
        "F",
        "Xs"
      ],
      "paramMapping": {
        "incoming": true,
        "var": "Xs",
        "node":"F"
      },
      "constraint": "(and (int (0 4) UUID_F) (= UUID_F ( ( sum(Xs) )/len(Xs) ) ) )"
    },
    "leafRule": {
      "param": "F",
      "constraint": "(int (0 4) UUID_F)"
    }
  }
},

“relationReificationTypes”, “relationReificationTranslationRules”, “relationReificationTypeDependentExpansions”, “relationReificationPropertySchema”, and “relationReificationExpansions”

In the case of RECOCOS, some of these relation reification elements also have a truth value, as is the case of claims, which therefore require supporting associating a boolean variable to the element itself (contrast the cardinality elements where the element itself has no meaning beyond the relation it reifies with Claims that do have their own truth value). With this in mind, and recognizing that the representation of certain aspects of the model are made more complex due to the limitations of mxGraph, we need to introduce additional constructs to, for example, disambiguate the types.

relationReificationTypes is, as before, a list representing the types that will be treated in this manner. Next, we come to the relationReificationTranslationRules, where we continue with the earlier pattern, and associate an object to each type we declared before. Here we have a parameter list (param) and a mapping for these parameters (paramMapping) that behave in precisely the same as in the case hierarchical types, with the difference being that we now make one mapping for incoming edges and one for outgoing, and not just one. Either of these can be a single edge, where we’d mark the mapping with "unique": true. Finally, another special characteristic of the constraints we can employ here, is the fact that we can have additional parameters that benefit from a lookup within the element’s attributes, as is the case of the Cardinality elements in RECOCOS.

To obtain, for example, the min value for the Cardinality elements, we define first in "relationReificationTypeDependentExpansions" the types that will have these additional expansions and then we provide a lookup schema in "relationReificationPropertySchema", which basically explains where to look in the element’s properties for the value to replace the placeholder with. This unfortunately means, that for now, at least, a minimal understanding of how the properties will be indexed by VariaMos is necessary. In addition, we define the more general expansions related to the nodes our element is connected with. In this case we declare that we will have the len and sum expansions mentioned in the subsection above.

Missing ::/2 and forall
It is worth noting that there are additional constructs that can be accessed within the constraint so that one can truly make use of every element of the model. The first of these is the edge(_) function, which allows one to refer specifically to the edge connecting to a particular element from the element we’re translating. Let’s examine in detail the case of the Claims. We have a constraint that reads:

(and (bool C) (iff (= C 1) (forall (x:Xs) (if (= x 1) (=< F edge(x)::Value) ) ) ) )

If we analyze this formula in detail, we can observe that we reference the edge of an x placeholder (whose nature will be detailed below). This x refers to another node in our model and, therefore, by invoking edge(x) in our template, we are referencing the edge (incoming or outgoing) to this node. Now, in this case in particular, we are interested in the value of the Value attribute set on this edge. We therefore introduce our second operator, the double colon :: operator, whose purpose is precisely that of giving access to a node’s attributes to generate a constraint. In this way, when we use the expression edge(x)::Value we will see the entire expression be replaced with whatever value we have set for the attribute in question. We must therefore be vigilant to only use attribute whose presence we are certain of.

In addition, in this formula, we also observe the expression forall (x:Xs). This expression is rather important, as it allows us to be able to refer to the specific elements of a given set of nodes without simply using expression expansions like sum or len. Specifically, what it allows us to do is construct the conjunction of the inner expression of the quantifier by instantiating the variable to each value in the set. In this case, since we quantify over Xs which represent the set of incoming edges, we will see each edge’s ID replace x in the set of conjuncts. Moreover, tying this to the edge and :: operators, we can make use of all the information of adjacent nodes in the graph.

"relationReificationTypes": [
  "Cardinality",
  "Claim",
  "SoftInfluence"
],
"relationReificationTranslationRules": {
  "Cardinality": {
    "param": [
      "F",
      "Xs",
      "min",
      "max"
    ],
    "paramMapping": {
      "inboundEdges": {
        "unique": false,
        "var": "Xs"
      },
      "outboundEdges": {
        "unique": true,
        "var": "F"
      }
    },
    "constraint": {
      "Cardinality": "(and (=< (F * min) (sum(Xs))) (= (sum(Xs)) (F * max)) )"
    }
  },
  "Claim": {
    "param": [
      "C",
      "F",
      "Xs"
    ],
    "paramMapping": {
      "node": "C",
      "inboundEdges": {
        "unique": false,
        "var": "Xs"
      },
      "outboundEdges": {
        "unique": true,
        "var": "F"
      }
    },
    "constraint": {
      "Claim": "(and (bool C) (iff (= C 1) (forall (x:Xs) (if (= x 1) (=< F edge(x)::Value) ) ) ) )"
    }
  },
  "SoftInfluence": {
    "param": [
      "S",
      "F",
      "Xs"
    ],
    "paramMapping": {
      "node": "S",
      "inboundEdges": {
        "unique": true,
        "var": "F"
      },
      "outboundEdges": {
        "unique": false,
        "var": "Xs"
      }
    },
    "constraint": {
      "SoftInfluence": "(and (bool S) (iff (= S 1) (if (= F edge(F)::Value) (forall (x:Xs) (= x edge(x)::SatisfactionLevel) ) ) ) )"
    }
  }
},
"relationReificationTypeDependentExpansions": {
  "Cardinality": {
    "Cardinality": [
      "max",
      "min"
    ]
  }
},
"relationReificationPropertySchema": {
  "min": {
    "index": 0,
    "key": "value"
  },
  "max": {
    "index": 1,
    "key": "value"
  }
},
"relationReificationExpansions": {
  "params": [
    "Xs"
  ],
  "functions": [
    "sum",
    "len"
  ]
},

“relationTypes” and “relationTranslationRules”

These rules are designed specifically to provide translations for edges between nodes in the model. We suppose the edges themselves have no variable associated to them and instead, we obtain two bindings. The first is that of the source of the edge and the second is always bound to the target of the edge. We can then use these nodes’ IDs in the constraint.

"relationTypes": [
  "SubGoal"
],
"relationTranslationRules": {
  "SubGoal": {
    "params": [
      "F1",
      "F2"
    ],
    "constraint": "(= UUID_F1 UUID_F2)"
  }
},

“ignoredRelationTypes” and “symbolMap”

For the sake of completeness, we must declare all model elements that do not have a specific translation and that is safe to ignore. We do this by referencing their types in “ignoredRelationTypes”.

In addition, before the translation is complete, it is possible that in our model we use symbols that do not translate well into the solvers and must therefore be replaced. In particular, for RECOCOS, we use “–“, “-“, “=”, “+”, and “++” to symbolize the scale 0-4. Since we cannot directly send these elements to the solver, it is necessary to transform them into their numeric counterparts. To do this, the translator makes an additional pass at the end of translation where it uses the symbolMap object to determine the replacements for all the symbols that are mentioned there.

"ignoredRelationTypes": [
  "SoftGoal_SoftGoal",
  "Claim_SoftGoal",
  "Cardinality_Goal",
  "SoftInfluence_SoftGoal",
  "ContextVariable_SoftInfluence",
  "Operationalization_Claim_Goal"
],
"symbolMap":{
  "++":"4",
  "+": "3",
  "=": "2",
  "-": "1",
  "--": "0"
}